【导师分享】苏文忠:探寻正立面体与球形镂空图案的关系与建模技巧
返回本文由铜陵市工业学校的苏文忠老师供稿
我们经常会看到镂空装饰球体的模型,在用三维软件建模时,曲面模型的控制不太容易,往往会使球表面图案变形,出现中间正常,两端变小等现象。如何使球表面图案的大小等大呢?根据欧拉定律,简单正多面体只有五种: 正四面体、正六面体、正八面体、正十二面体和正二十面体,今天我们以这五个正多面体分别来探讨下其中的规律。
先看效果图(图案可以自己任意编排)

我们知道正立面体的各角点正好外接球体,并且正多面体各个面全等,看下图

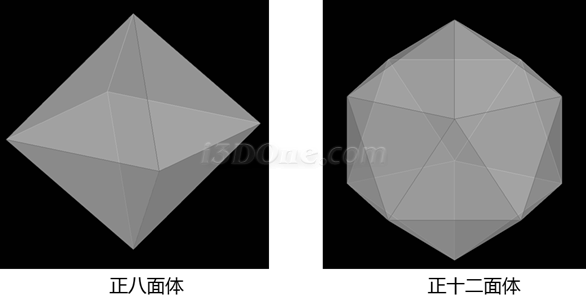
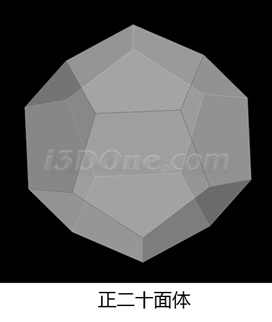
通过上面正立面体与球体的图示,我们只要知道正立面体棱长与球体半径的关系后,在正立面体各个面上绘制相应图案后,利用3DOne软件的投影曲线和曲面分割命令,将各个面上绘制的图案投影到球体上,将不需要的面删除,最后再利用抽壳命令即可生成立体等大图案的模型。
因为正立面体和球体都是我们必须要的,正立面体的各个面便于我们绘制图案,而球体是作为投影曲线用的,问题的重点是棱长已知,球体的半径如何求?我们可以运用数学的知识的求解,但是在3DOne软件中,这个问题很好解决,看下面所作辅助线。
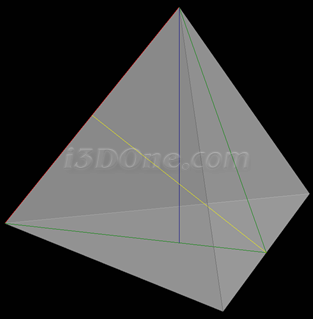
正四面体,蓝线与黄线交点为球心,蓝线上半部分为半径,红线为棱长

正六面体,绿线为球体直径
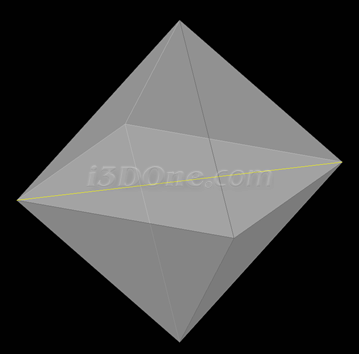
正八面体,黄线为球体直径
一、以正四面体为例看如何制作等大图案的球体镂空效果:
1.看上图正四面体的辅助线,在3DOne中绘图,先绘制边长为100(此为红线棱长长度)的正三角形,作出高线,高线即为上图中绿线的长度(利用3DOne距离测量工具测得长度为86.60254,如下图:
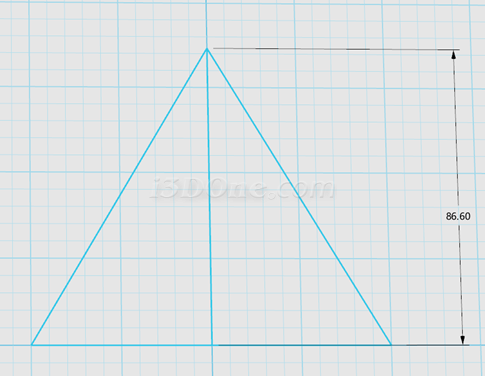
2.在旁边继续画一水平线长度为86.60254,以直线两端点分别画半径100和半径86.60254两个圆,如图
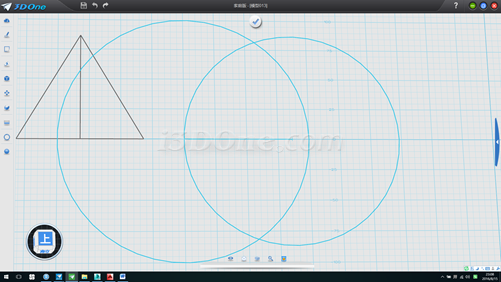
3.连接线段,并作出两条高线,删除两辅助圆,如图
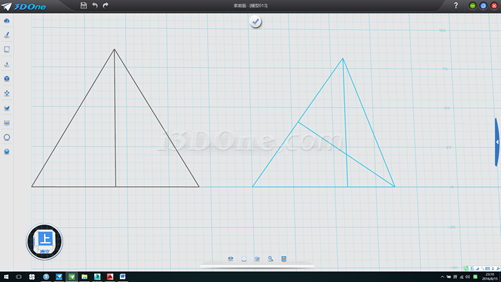
4.分别测得垂直高线的两段长为61.2372(此为球半径)和20.41241
5.删除所有辅助线(为避免干拢后期作图),画100长直线,分别以两端点画半径为100的圆,连接线段,如图
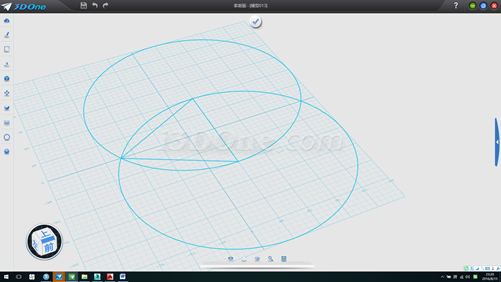
6.作两高线,删除辅助圆,将草图两高线交点处移至(0,0)点,如图
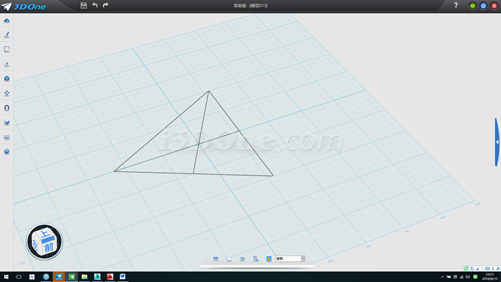
7.沿辅助线再描一边长100的三角形并下移20.41241,如图
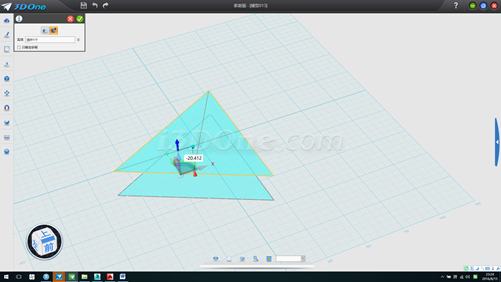
8.水平画一长61.11056长的线段,旋转90度,移动使下端点位于(0,0)处,如图
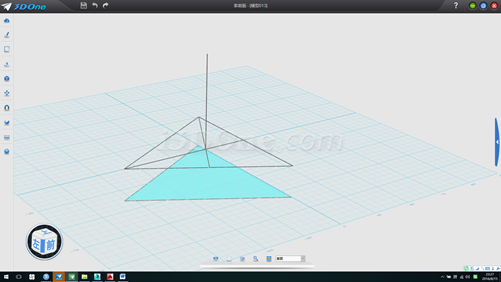
9.沿辅助图形中一高线画一直线(可画长点以便于选择)并向上拉伸一平面,如图
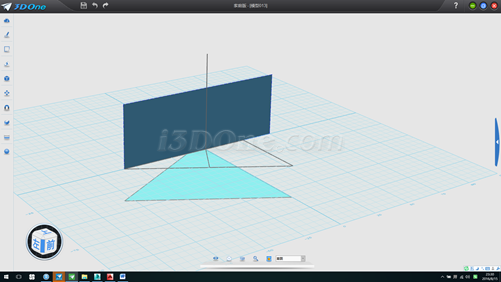
10.以此面为基准面画直线连接两线段端点,如图:
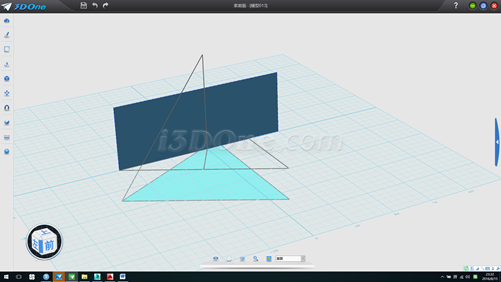
11.删除辅助线和面,环形阵列刚画的线,方向(0,0,1)数量3个,如图
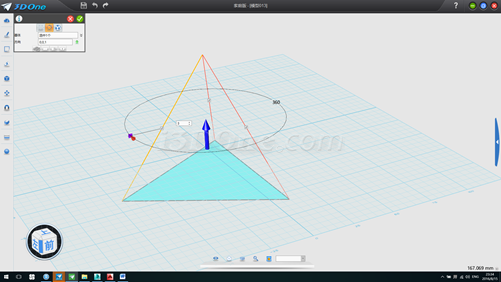
12.分别执行放样命令(注意连续方式选择无,如连续方式为灰色不可选则默认)四次即可求得正四面体形状,且重心位于(0,0),(若底面不能放样,则将底部三角形草图删除,以边形式放样即可)如图:
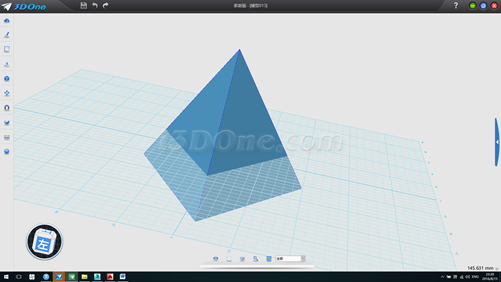
13.分别以两个面为基准面绘制图案,此例以画一弧为例说明,如图
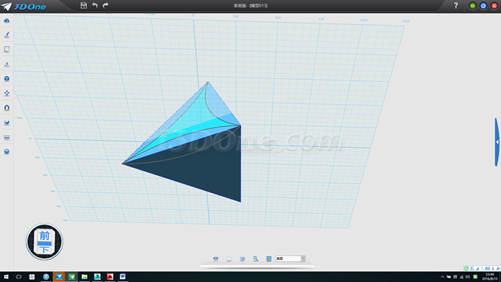
环形阵列,中心点(0,0,1),数量3个,如图
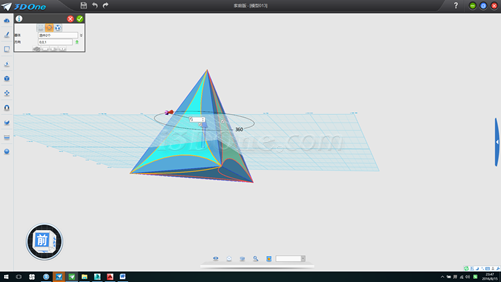
14.删除四个辅助面,并以(0,0)为球心作半径61.2372的球,将渲染模式设为线框模式(或者按CTRL+F),如图
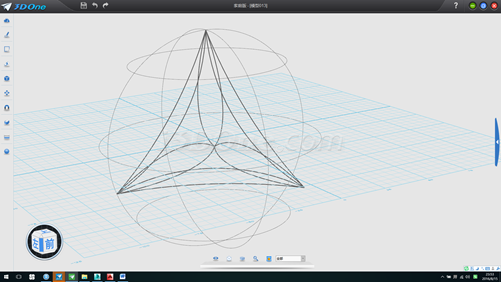
15.使用投影曲线命令将草图投影 球表面,并使用曲面分割命令对球表面进行分割,如图
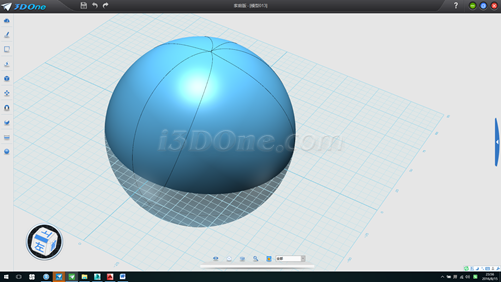
16.删除不需要的面,使用抽壳命令给模型增加厚度,如图
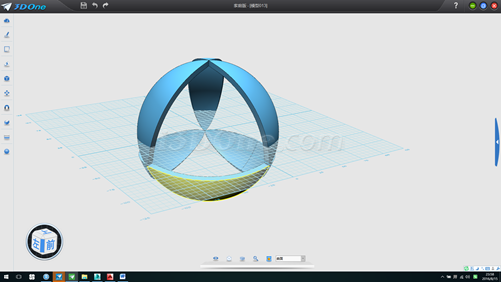
观察一下,是不是每个形状都是一样大呢。
同理,正立面体做法如下:
1.以(0,0)画长宽高分另为100的正方体,使用距离测量工具测得正方体两对角点距离为173.2051,此为球体直径长度,如图
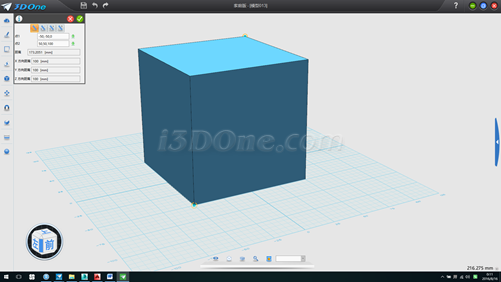
2.分别在六个面上绘制图案如图
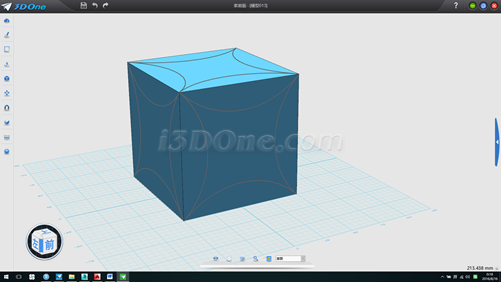
3.删除六面体,以(0,50)为球心作半径为86.60255为球体,后面的步骤同正四面体,最终效果如图
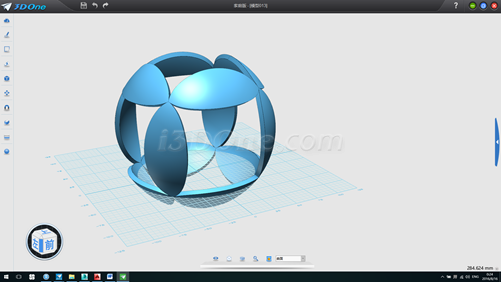
正八面体做法如下
1.画边长100的正方形,并将中心移至(0,0)退出草图模式,如图
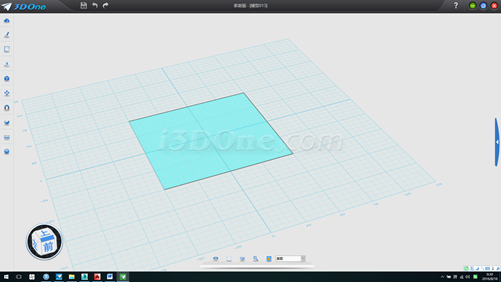
2.连接对角线(对角线一半长度70.71068即为球半径),删除正方形,向上拉伸对角线高度100,并以此拉伸面为基准面分别在刚才对角线两端点画半径100的圆,如图
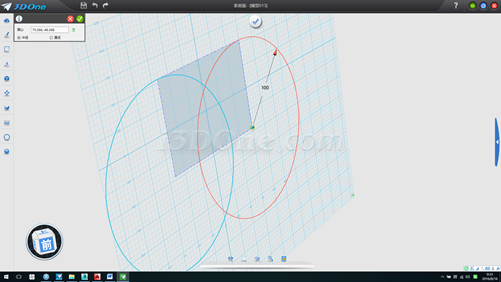
3.连接线段并删除辅助圆,退出草图模式,删除基准面,如图
4.环形阵列,方向(0,0,1),数量4个,如图
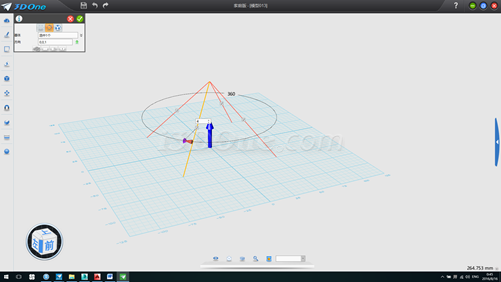
5. 再次环形阵型列,方向(1,0,0),数量2个,如图
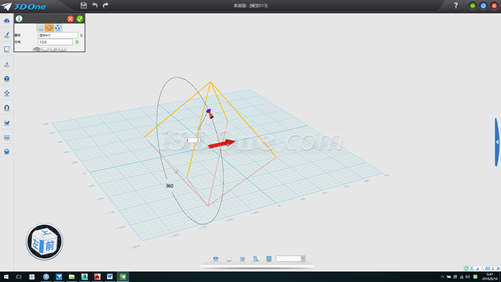
6.放样,后面步骤同正四面体,最终效果如下:
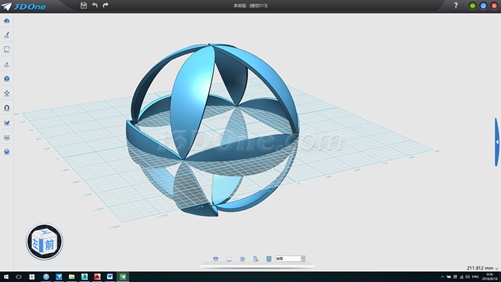
正十二面体的做法复杂些(其中涉及数学知识我们不深入讨论了)
1.先以(0,0)为圆心画正五边形,半径为50,再画另外两个半径50的五边形,旋转36度并移动至合适位置,如图
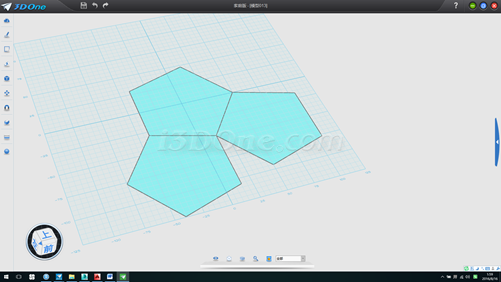
2.分别以两个五边形角点向另一五边形的边作垂线,如图
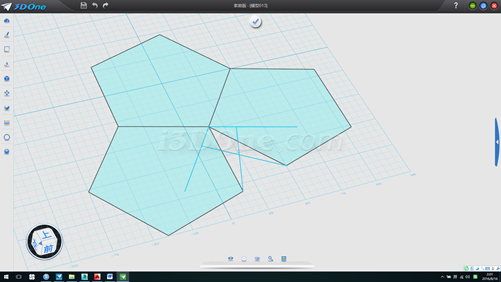
3.测得垂线长度55.9017,修剪,如图
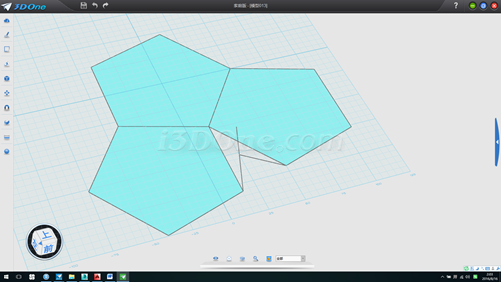
4. 拉伸所绘线高度100,以此拉伸面为基准面,以垂足点为圆心画半径55.9017的圆,以交点为起点向上画一直线,如图
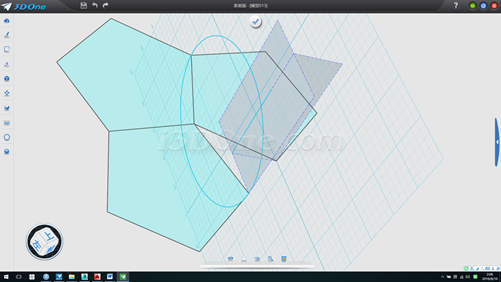
5.修剪线段冒头部分,删除圆和拉伸面,如图
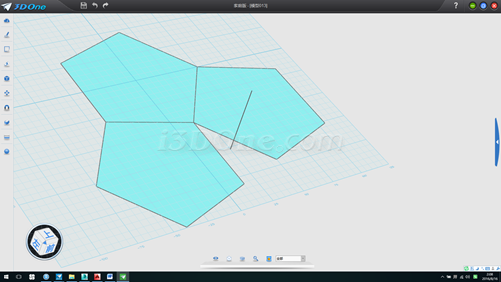
6.在平面上画一线段,如图
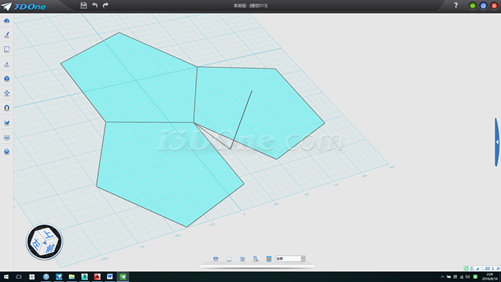
7.放样,并以此放样面为基准面画一斜线(红线位置),测得斜线长度58.77853,此为五边形边长的长度,如图
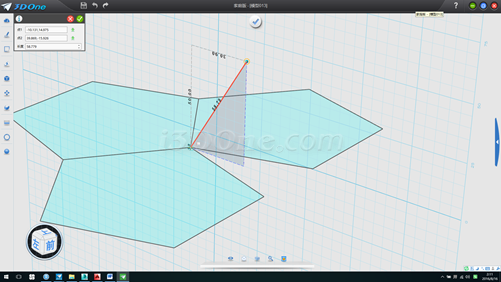
8.删除基准面,环形阵列斜线2个,角度为-72度,方向(0,0,1)如图
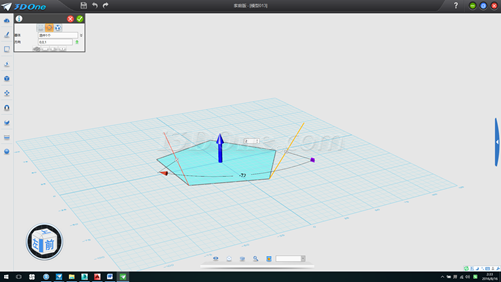
9.放样两根线作为基准面,以此基准面上两个端点画两个半径为58.77853的圆,如图
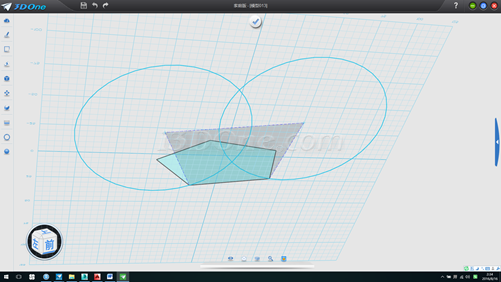
10.连五条线构成五边形,删除辅助圆和基准面,如图
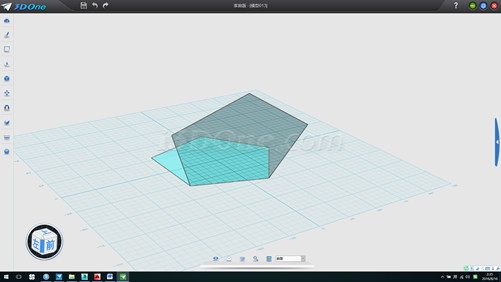
11.分别将两五边形向上向内拉伸若干,然后删除多余面,如图
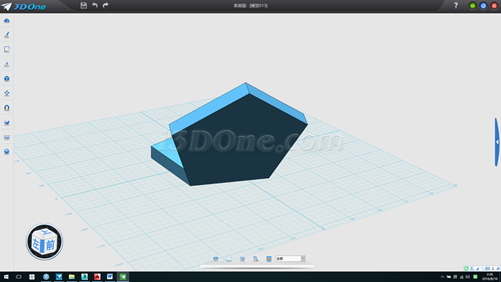
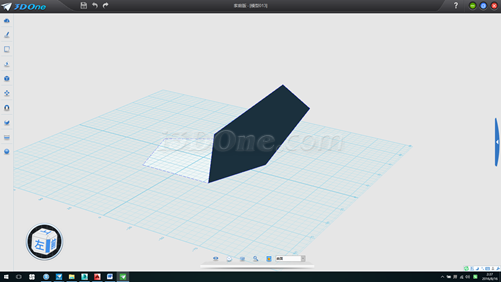
12.将斜平面环形阵型列五个,方向(0,0,1)角度360,如图
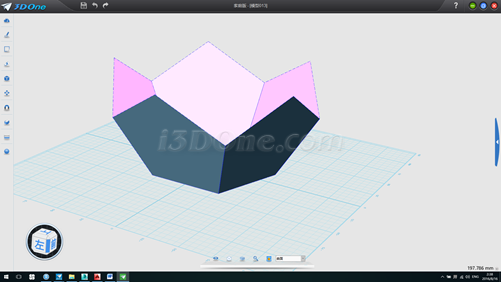
13.再次将六个物体环形阵列,方向(1,0,0),数量2个,如图
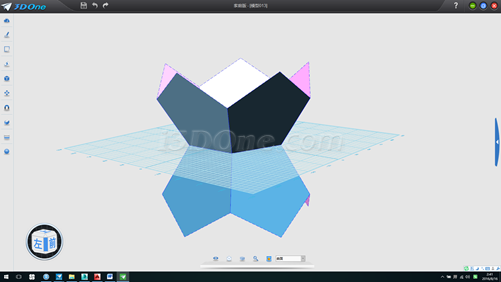
14.将阵列的六个上移,然后旋转36度,再移至合适位置即可构成正十二面体,如图
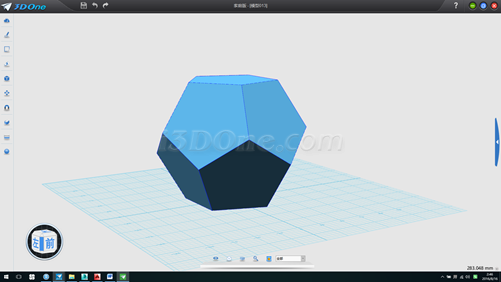
15.接下来我们找球心及球半径,按CTRL+F转线框模式,在最下方的五边形内画一条线,如图
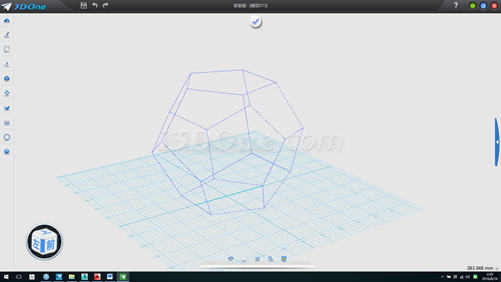
16.将此线向上拉伸高于整个多面体,并以此拉伸面作为基准面画线连接图上左右两个顶点,此线即为球体直径长度,测得直径一半长度为82.36391,中心即为球心,如图
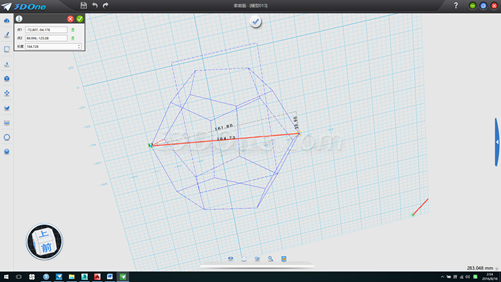
17.选择所有物体,移动,以直线中心为起始点,目标点为(0,0),删除直线和辅助面,如图
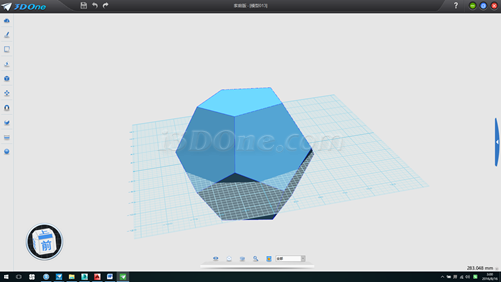
18.其他步骤同上,效果如下
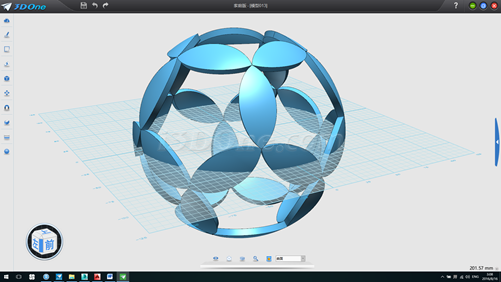
最后我们来看正二十面体是如何制作出来的
1.以(0,0)为圆心画半径50的正五边形,距离测量边长为58.77853,作辅助线,如图
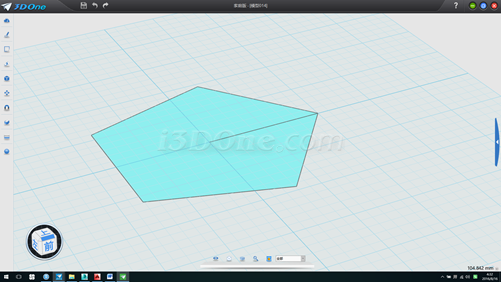
2.先隐藏五边形,向上拉伸直线,以拉伸的面为基准面画半径为58.77853的圆和从(0,0)点向上画一直线,如图
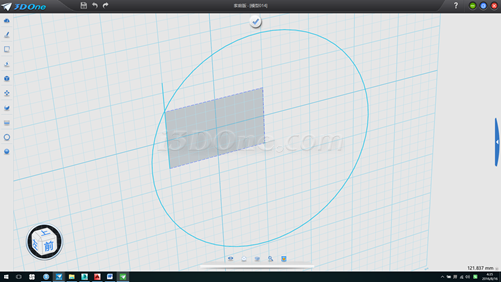
3.修剪直线,并删除圆,如图
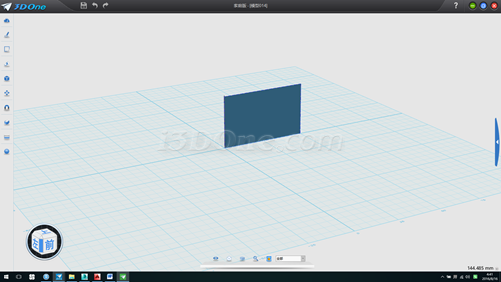
4.将隐藏物体显示,放样,放样类型为起点到轮廓,连续方式为无,如图
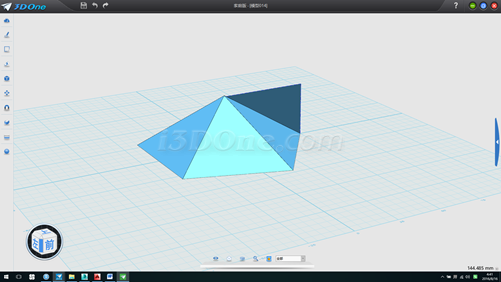
5.删除底部平面,再以刚拉伸面为基准面,作辅助线,如图
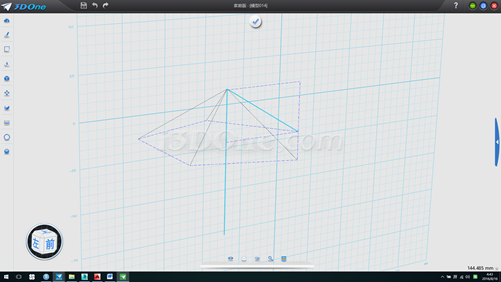
6.将斜线绕自身中心旋转90度,并使用修剪、延伸曲线命令,然后再利用修剪命令修剪多余线段,如图
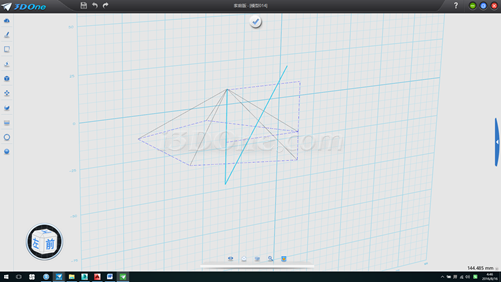
7.删除斜线,垂线即为球的半径,测得长度为55.90119,将拉伸面绕X轴旋转90度,并移至垂线下端点对齐,将五面体以拉伸面为镜像平面镜像到下面,如图
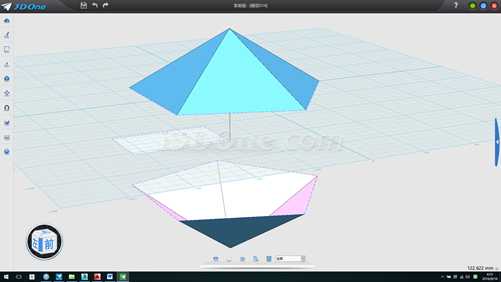
8.将上面五面体绕Z轴旋转36度,并移动它使顶点与垂线顶点对齐,选择所有物体,移动使垂线下端点作为起始点,目标点为(0,0),删除拉伸面,如图
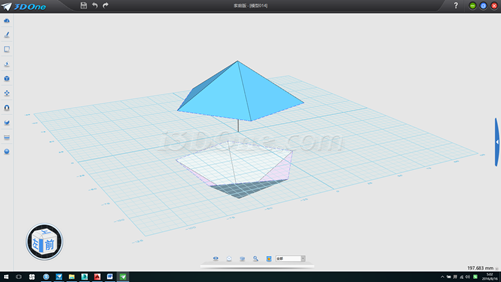
9.拉伸垂线,方向(1,0,0),如图
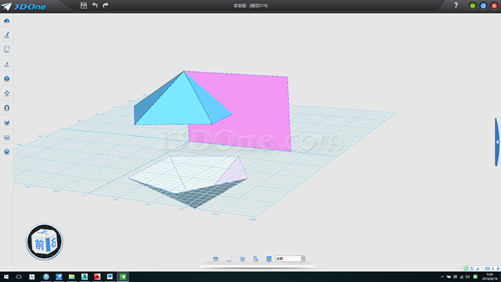
10.以此拉伸面为基准面,作辅助线,删除辅助面,如图
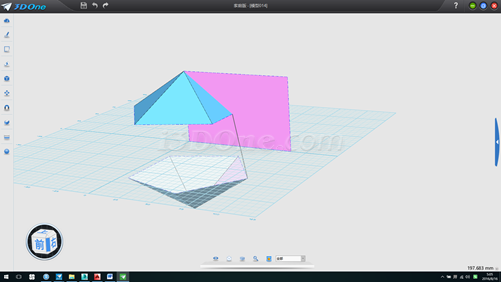
11. 拉伸辅助线,方向为上五面体的边,如图
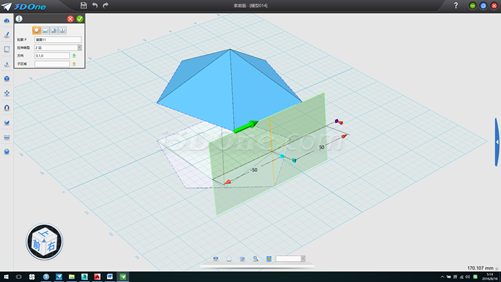
12.以此拉伸面为基准面分两次画两线段,如图
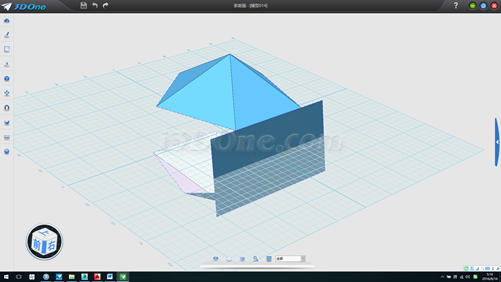
13.将拉伸面环形阵列,方向(0,0,1),数量2个,角度-72度,并以此拉伸面为基准面画一条线段,如图
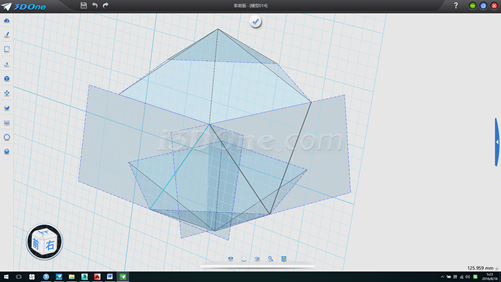
14.删除两基准面,分别放样出两个平面,注意放样连续方式为无或默认不可选,如出现面反向(粉红色表示)不影响,如图
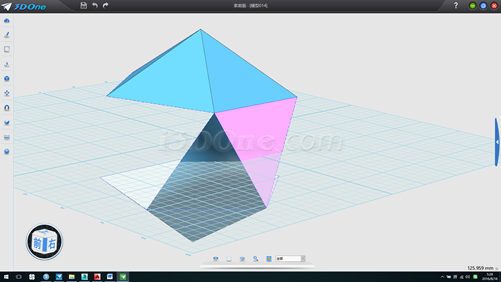
15.环形阵列两个放样面,方向(0,0,1)数量5个,角度360,如图
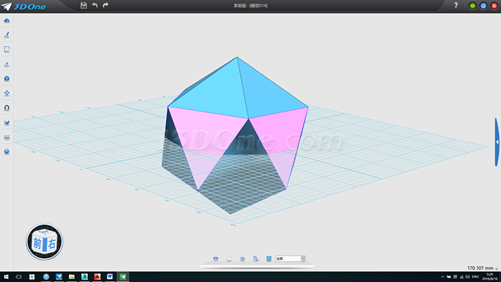
16. 其他步骤同上,效果如下
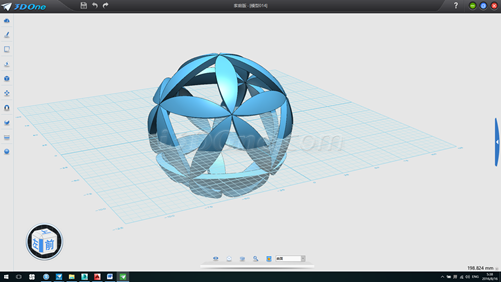
无论是利用正四面体还是正十二面体制作等大图案的球形镂空,原理都是一样的。在建模过程中,动用数学的思维除了能够帮助理解,还能起到事半功倍的效果。













